2021年度　金沢大学入試問題　回答例(数学大問３？)

今年（2021年度）金沢大学入試の数学の問題を小耳にはさんだので挑戦してみました．

お約束ですが，以下の回答例はあくまで個人の見解で、その上正しいという保証は全くありませんのであしからず．また，この回答に対するご意見(ここ違うだろ、とか、計算違うぞ、など)もなんでも受け付けますので，何かありましたらコメントください．

話に聞いた問題(おそらく大問３とのこと)の内容は大体以下の通りです．

“半径１、高さ１の円柱があり、底面の直径を横切り、底面と30°の角を成す平面が切り取る円柱の小さい方の体積を求めよ．”

おおよその方針は，断面積Sを変数（この場合はθ）で表して、積分するというもの．積分する微小体積がS・dsinθみたいになるので、その辺りから積分の計算問題になってくるのかな、という印象です．dsinθを(dsinθ/dθ)・dθに直して、進めます．部分積分を使うまでもなく、sin^2+cos^2=1を使うと積分可能な形になるので、素直に積分して答えらしきものが出てきます．

答えとしては悪くない気がするんですが，円の要素がある立体なのに、答えにπが含まれてないのが不可解です．やっぱり間違ってるのかも…？

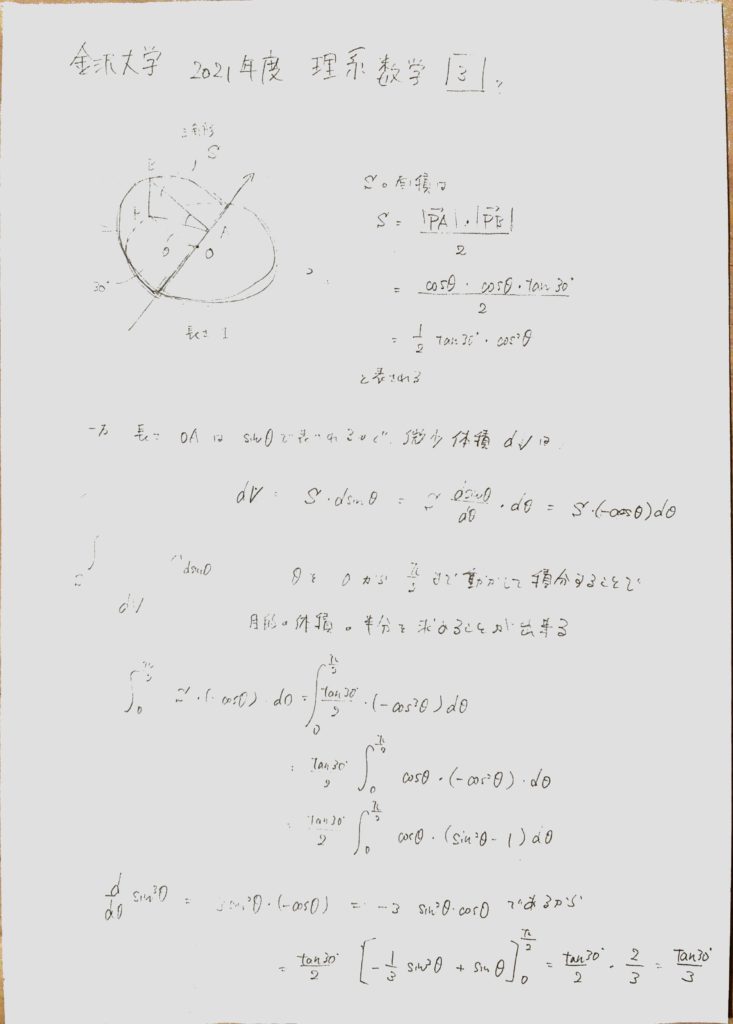
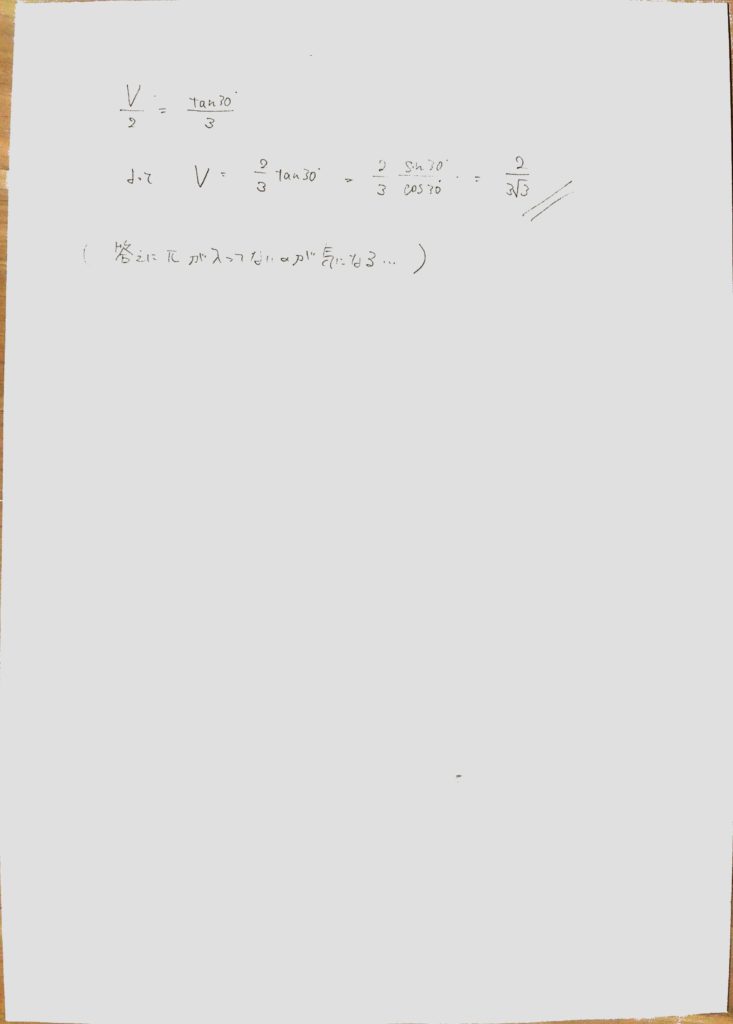
せっかくやるなら合格発表直前じゃなくて、試験直後に挑戦してみればよかったですね．

他には数列の問題が大問２つ分くらいでたとかでないとか．問題が手に入ったらトライしてみたいと思います(でも、解けない可能性大)．

最近はAIの損失関数とかロボットの座標計算とか，仕事でも数学っぽい内容を使う機会が増えてきていますので、こういう問題がサラッと解ける方，大歓迎です．